WP1 Ideas for project to pursue: Difference between revisions
| Line 22: | Line 22: | ||
Local-to-Global MC is a method that was introduced in the early 90's for electron transport simulations for electron radiotherapy treatment planning systems. The idea was to gain speed in MC calculations of the dose distribution. The method is based on simulations of electron transport in local geometries, so-called "kugels", i.e. "spheres", of varying material compositions, dimensions and obviously, electron energies. In its simplest form, ignoring secondary particle production, electrons are initiated at the center of a given "kugel". The electron exit angles, positions and energies, i.e. the exiting electron's "phase space", are then tallied. The procedure is repeated for different materials, "kugel" sizes and electron energies. The resulting distributions are stored in memory generating the so-called probability distribution functions. Then, in the global geometry, the electron simulations are accelerated through the use of these "kugels" and the corresponding probability distributions from which random samples are drawn. The method has previously been successfully applied to electron radiotherapy. More on the results and the method itself can be found here https://digital.library.unt.edu/ark:/67531/metadc682086/m2/1/high_res_d/39026.pdf. The Local-to-Global MC methods have, however, been abandoned due to the affordability of powerful CPUs and GPUs. | Local-to-Global MC is a method that was introduced in the early 90's for electron transport simulations for electron radiotherapy treatment planning systems. The idea was to gain speed in MC calculations of the dose distribution. The method is based on simulations of electron transport in local geometries, so-called "kugels", i.e. "spheres", of varying material compositions, dimensions and obviously, electron energies. In its simplest form, ignoring secondary particle production, electrons are initiated at the center of a given "kugel". The electron exit angles, positions and energies, i.e. the exiting electron's "phase space", are then tallied. The procedure is repeated for different materials, "kugel" sizes and electron energies. The resulting distributions are stored in memory generating the so-called probability distribution functions. Then, in the global geometry, the electron simulations are accelerated through the use of these "kugels" and the corresponding probability distributions from which random samples are drawn. The method has previously been successfully applied to electron radiotherapy. More on the results and the method itself can be found here https://digital.library.unt.edu/ark:/67531/metadc682086/m2/1/high_res_d/39026.pdf. The Local-to-Global MC methods have, however, been abandoned due to the affordability of powerful CPUs and GPUs. | ||
An important point is, however, that the method could, in principle, be applied to the Most-Likely Path (MLP) estimation in proton CT. "Kugels" of varying materials and sizes can be simulated with varying proton energies to generate probability distributions. These local geometries can then be used to track protons through the patient geometry. It will be a tedious step to generate the required probability distributions. However, it would be of utmost interest to implement this idea and compare it to conventional techniques used for the MLP estimations such as those based on log-likelihood maximization. | An important point is, however, that the method could, in principle, be applied to the Most-Likely Path (MLP) estimation in proton CT. "Kugels" of varying materials and sizes can be simulated with varying proton energies to generate probability distributions. These local geometries can then be used to track protons through the patient geometry. An obvious advantage of the method over the more conventional methods would be the possibility of taking into account heterogeneous patient geometries. It will be a tedious step to generate the required probability distributions. However, it would be of utmost interest to implement this idea and compare it to conventional techniques used for the MLP estimations such as those based on log-likelihood maximization. | ||
Revision as of 21:17, 22 November 2017
Below is a list of ideas regarding DTC data analysis, design etc. that might be worthwhile to pursue.
Time-dependence of charge diffusion process
We see in the ALPIDE chips that the quick integration time of ~10 µs reveals a time dependence on the charge diffusion process -- i.e. that too small clusters, medium clusters and then large clusters with holes are visible. It would be interesting to see if it's possible to use the data already acquired to model the time dependency in this process.
Re-implementation of Maczewski model to analytically describe charge diffusion process
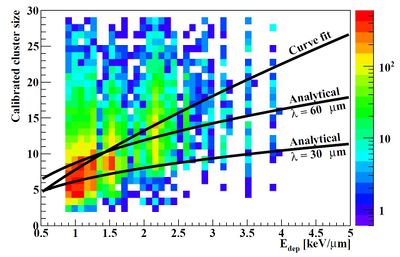
The model as it stands today looks like below, which does not accurately describe the data.
Two shortcomings of the Maczewski model (see his thesis and Even's MSc thesis) are that
- Only one term in the expansion is used (the model was used as in Maczewski's thesis)
- The Most Probable Value of the Landau distribution of Energy Deposition values in the epitaxial value was considered. This is a more serious approximation, and a new implementation should be made based on Even's code that rather samples from a Landau distribution.
PID for DTC
Intuitively, it should be possible to perform a PID (Particle ID) together with the track reconstruction in the DTC. Different particles (w/different charge) should have a different edep distribution in the epitaxial layer, giving rise to depth-dependent cluster size distributions (depth dose) of different values. The height of the plataeu region of the Bragg Curve is then the PID indicator: H, He, C, ... This would e.g. be of help during alpha beam tests, where secondary protons from the phantom easily could be removed.
- Helge wants to further explore this idea and if good make a conference paper on this + the charge diffusion model modeled on the data we already have -- and/or on ALPIDE.
- Bias voltage dependency..?
Local-to-Global Monte Carlo simulations for quick MLP
Local-to-Global MC is a method that was introduced in the early 90's for electron transport simulations for electron radiotherapy treatment planning systems. The idea was to gain speed in MC calculations of the dose distribution. The method is based on simulations of electron transport in local geometries, so-called "kugels", i.e. "spheres", of varying material compositions, dimensions and obviously, electron energies. In its simplest form, ignoring secondary particle production, electrons are initiated at the center of a given "kugel". The electron exit angles, positions and energies, i.e. the exiting electron's "phase space", are then tallied. The procedure is repeated for different materials, "kugel" sizes and electron energies. The resulting distributions are stored in memory generating the so-called probability distribution functions. Then, in the global geometry, the electron simulations are accelerated through the use of these "kugels" and the corresponding probability distributions from which random samples are drawn. The method has previously been successfully applied to electron radiotherapy. More on the results and the method itself can be found here https://digital.library.unt.edu/ark:/67531/metadc682086/m2/1/high_res_d/39026.pdf. The Local-to-Global MC methods have, however, been abandoned due to the affordability of powerful CPUs and GPUs.
An important point is, however, that the method could, in principle, be applied to the Most-Likely Path (MLP) estimation in proton CT. "Kugels" of varying materials and sizes can be simulated with varying proton energies to generate probability distributions. These local geometries can then be used to track protons through the patient geometry. An obvious advantage of the method over the more conventional methods would be the possibility of taking into account heterogeneous patient geometries. It will be a tedious step to generate the required probability distributions. However, it would be of utmost interest to implement this idea and compare it to conventional techniques used for the MLP estimations such as those based on log-likelihood maximization.