Software for design optimization
Required software
In order to run the software to generate the geomtry, Monte Carlo data and do full simulations, you need the following software:
- ROOT
- Geant4
- Gate
- DTC toolkit (Helge's code)
GATE Simulations
Generating the geometry
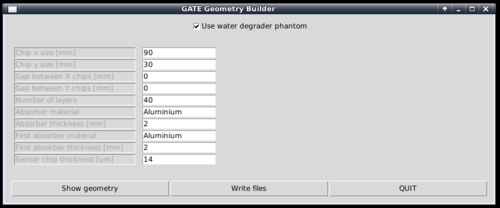
To generate the geometry files to run in Gate, a Python script is supplied. It is located within the gate/python subfolder.
[gate/python] $ python gate/python/makeGeometryDTC.py
Choose the wanted characteristics of the detector, and use write files in order to create the geometry file Module.mac, which is automatically included in Main.mac. Note that the option "Use water degrader phantom" should be checked (as is the default behavior)!
Creating the full simulations files for a range-energy look-up-table
It is not critical to have a high number of primaries in this part. 5000-10000 is enough for this step. To loop through different energy degrader thicknesses, run the script runDegrader.sh:
[gate/python] $ ./runDegraderFull.sh <absorber thickness> <degraderthickness from> <degraderthickness stepsize> <degraderthickness to>
The brackets indicate the folder in the Github repository to run the code from. Please note that the program should not be executed using the sh command, as this refers do different shells in different Linux distribtions, and not all shells support the conditional bash expressions used in the script.
For example, with a 3 mm degrader, and simulating a 250 MeV beam passing through a phantom of 50, 55, 60, 65 and 70 mm water:
[gate/python] $ ./runDegraderFull.sh 3 50 5 70
Please note that there is a variable NCORES in this script, which ensures that NCORES versions of the Gate executable are run in parallel, and then waits for the last background process to complete before a new set of NCORES executables are run. So if you set NCORES=8, and run sh runDegraderFull.sh 3 50 1 70, first 50-57 will run in parallel, and when they're done, 58-65 will start, etc. The default value is NCORES=4.
Creating the chip-readout simulations files for resolution calculation
A sub 1-mm step size will really tell us if we manage to detect such small changes in a beam energy. Loop through the different absorber thicknesses:
[gate/python] $ ./runDegrader.sh <absorber thickness> <degraderthickness from> <degraderthickness stepsize> <degraderthickness to>
The same parallel-in-sequential run mode has been configured here.
Creating the basis for range-energy calculations
The range-energy look-up-table
Now we have ROOT output files from Gate, all degraded differently through a varying water phantom and therefore stopping at different places in the DTC. We want to follow all the tracks to see where they end, and make a histogram over their stopping positions. This is of course performed from a looped script, but to give a small recipe:
- Retrieve the first interaction of the first particle. Note its event ID (history number) and edep (energy loss for that particular interaction)
- Repeat until the particle is outside the phantom. This can be found from the volume ID or the z position (the first interaction with {math|z>0}). Sum all the found edep values, and this is the energy loss inside the phantom. Now we have the "initial" energy of the proton before it hits the DTC
- Follow the particle, noting its z position. When the event ID changes, the next particle is followed, and save the last z position of where the proton stopped in a histogram
- Do a Gaussian fit of the histogram after all the particles have been followed. The mean value is the range of the beam with that particular "initial" energy. The spread is the range straggling. Note that the range straggling is more or less constant, but the contributions to the range straggling from the phantom and DTC, respectively, are varying linearly.
This recipe has been implemented in DTCToolkit/Scripts/findRange.C. Test run the code on a few of the cases (smallest and biggest phantom size ++) to see that
- The correct start- and end points of the histogram looks sane. If not, this can be corrected for by looking how
xfromandxtois calculated and playing with the calculation. - The mean value and straggling is calculated correctly
- The energy loss is calculated correctly
You can run findRange.C in root by compiling and giving it three arguments; Energy of the protons, absorber thickness, and the degrader thickness you wish to inspect.
[DTCToolkit/Scripts] $ root ROOT [1] .L findRange.C+ // void findRange(Int_t energy, Int_t absorberThickness, Int_t degraderThickness) ROOT [2] findRange f(250, 3, 50); f.Run();
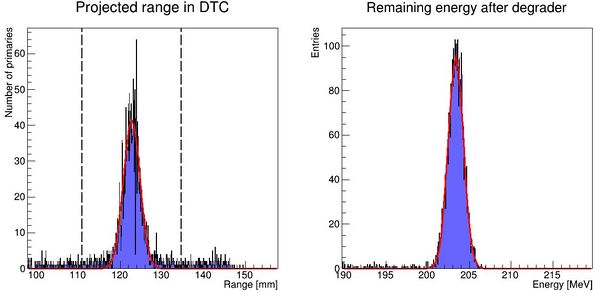
The output should look like this: Correctly places Gaussian fits is a good sign.
If you're happy with this, then a new script will run findRange.C on all the different ROOT files generated earlier.
[DTCToolkit/Scripts] $ root ROOT [1] .L findManyRangesDegrader.C // void findManyRanges(Int_t degraderFrom, Int_t degraderIncrement, Int_t degraderTo, Int_t absorberThicknessMmFrom, Int_t absorberThicknessMmIncrement, Int_t absorberThicknessMmTo) ROOT [2] findManyRanges(50, 5, 70, 3, 1, 3)
This is a serial process, so don't worry about your CPU.
The output is stored in DTCToolkit/Output/findManyRangesDegrader.csv.
It is a good idea to look through this file, to check that the values are not very jumpy (Gaussian fits gone wrong).
We need the initial energy and range in ascending order. The findManyRangesDegrader.csv files contains more rows such as initial energy straggling and range straggling for other calcualations. This is sadly a bit tricky, but do (assuming a 3 mm absorber geometry):
[DTCToolkit] $ cat OutputFiles/findManyRangesDegrader.csv | awk '{print ($6 " " $3)}' | sort -n > Data/Ranges/3mm_Al.csv
NB: If there are many different absorber geometries in findManyRangesDegrader, either copy the interesting ones or use | grep " X " | to only keep X mm geometry
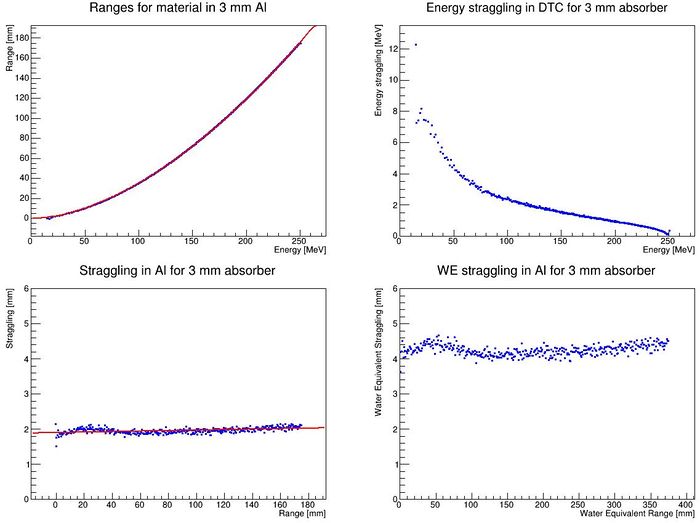
When this is performed, the range-energy table for that particular geometry has been created, and is ready to use in the analysis. Note that since the calculation is based on cubic spline interpolations, it cannot extrapolate -- so have a larger span in the full Monte Carlo simulation data than with the chip readout. For more information about that process, see this document: File:Comparison of different calculation methods of proton ranges.pdf
Range straggling parameterization and [math]\displaystyle{ R_0 = \alpha E^p }[/math]
It is important to know the amount of range straggling in the detector, and the amount of energy straggling after the degrader. In addition, to calculate the parameters [math]\displaystyle{ \alpha, p }[/math] from the somewhat inaccurate Bragg-Kleeman equation [math]\displaystyle{ R_0 = \alpha E ^ p }[/math], in order to correctly model the "depth-dose curve" [math]\displaystyle{ dE / dz = p^{-1} \alpha^{-1/p} (R_0 - z)^{1/p-1} }[/math]. This is done by fitting the Bragg-Kleeman equation to the range-energy look up tables found by using DTCToolkit/Scripts/findManyRangesDegrader.C.
To find all this, run the script DTCToolkit/Scripts/findAPAndStraggling.C. This script will loop through all available data lines in the DTCToolkit/OutputFiles/findManyRangesDegrader.csv file that has the correct absorber thickness, so you need to clean the file first (or just delete it before running findManyRangesDegrader.C).
[DTCToolkit/Scripts] $ root ROOT [0] .L findAPAndStraggling.C+ // void findAPAndStraggling(int absorberthickness) ROOT [1] findAPAndStraggling(3)
The output from this function should be something like this:
In addition, the following parameters should be extracted:
Bragg-Kleeman parameters: R = 0.011626 E ^ 1.743151 Straggling = 1.8568 + 0.000856 R
Running the DTC Toolkit
Configuring the DTC Toolkit to run with correct geometry
The values from findManyRanges.C should already be in DTCToolkit/Data/Ranges/3mm_Al.csv (or the corresponding material / thickness). Check that the file is correctly loaded in the file DTCToolkit/GlobalConstants/MaterialConstants.C. The values from findAPAndStraggling.C are put into the same file DTCToolkit/GlobalConstants/MaterialConstants.C:
81 void createSplines() {
...
107 else if (kAbsorbatorThickness = 3) {
108 in.open("Data/Ranges/3mm_Al.csv");
109 }
...
192 else if (kAbsorbatorThickness = 3) {
193 alpha_aluminum = 0.011626;
194 p_aluminum = 1.743151;
195 straggling_a = 1.8568;
196 straggling_b = 0.000856;
197 }
Or in the corresponding material (alpha_pmma, alpha_carbon, etc.) and absorbatorthickness lines.
And in the file DTCToolkit/Scripts/makePlots.C, put the \alpha, p parameters.
144 else if (absorberThickness == 3) {
145 a_dtc = 0.011626;
146 p_dtc = 1.743151;
147 }
Then, look in the file DTCToolkit/GlobalConstants/Constants.h and check that the correct absorber thickness values etc. are set:
... 39 Bool_t useDegrader = true; ... 52 const Float_t kAbsorberThickness = 3; ... 59 Int_t kEventsPerRun = 100000; ... 66 const Int_t kMaterial = kAluminum;
Since we don't use tracking but only MC truth in the optimization, the number kEventsPerRun ([math]\displaystyle{ n_p }[/math] in the NIMA article) should be higher than the number of primaries per energy.
How does the DTC Toolkit calculate resolution?
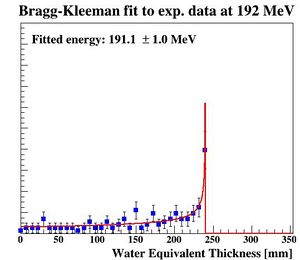
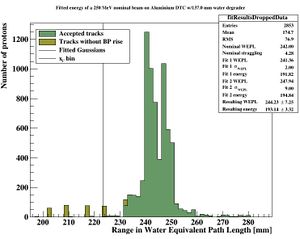
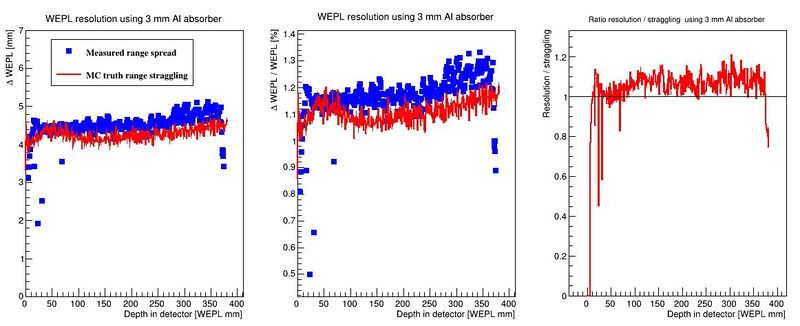
The resolution in this case is defined as the width of the final range histogram for all protons. The goal is to match the range straggling which manifests itself in the Gaussian distribution of the range of all protons in the DTC, from the full Monte Carlo simulations:
To characterize the resolution, a realistic analysis is performed. Instead of scoring the complete detector volume, including the massive energy absorbers, only the sensor chips placed at intervals ([math]\displaystyle{ \Delta z = 0.375\ \textrm{mm} + d_{\textrm{absorber}} }[/math]) are scored. Tracks are compiled by using the eventID tag from GATE, so that the track reconstruction efficiency is 100%. Each track is then put in a depth / edep graph, and a Bragg curve is fitted on the data:
The distribution of all fitted ranges (simple to calculate from fitted energy) should match the distribution above - with a perfect system. All degradations during analysis, sampling error, sparse sampling, mis-fitting etc. will ensure that the peak is broadened.
PS: Please forgive me the fact that the first figure is given in projected range, the second figure is given in initial energy and the third figure is given in projected water equivalent range...... They are converted losslessly since LUTs are used.
Finding the resolution
To find this resolution, or degradation in the straggling width, for a single energy, run the DTC toolkit analysis.
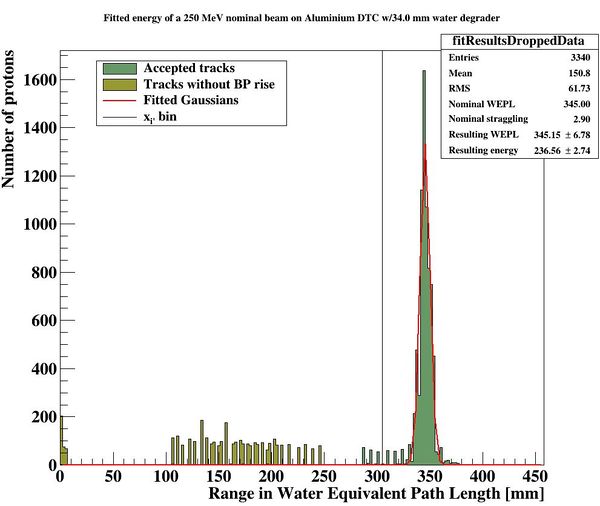
[DTCToolkit] $ root Load.C // drawBraggPeakGraphFit(Int_t Runs, Int_t dataType = kMC, Bool_t recreate = 0, Float_t energy = 188, Float_t degraderThickness = 0) ROOT [0] drawBraggPeakGraphFit(1, 0, 1, 250, 34)
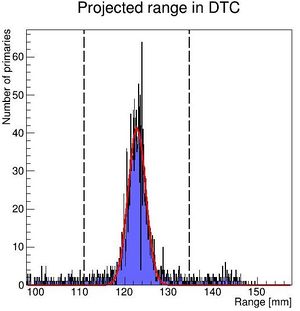
This is a serial process, so don't worry about your CPU when analysing all ROOT files in one go. With the result
The following parameters are then stored in DTCToolkit/OutputFiles/results_makebraggpeakfit.csv:
| Absorber thickness | Degrader thickness | Nominal WEPL range | Calculated WEPL range | Nominal WEPL straggling | Calculated WEPL straggling |
| 3 (mm) | 34 (mm) | 345 (mm WEPL) | 345.382 (mm WEPL) | 2.9 (mm WEPL) | 6.78 (mm WEPL) |
To perform the analysis on all different degrader thicknesses, use the script DTCToolkit/makeFitResultPlotsDegrader.sh (arguments: degrader from, degrader step and degrader to):
[DTCToolkit] $ sh makeFitResultsPlotsDegrader.sh 1 1 380
This may take a few minutes... When it's finished, it's important to look through the file results_makebraggpeakfit.csv to identify all problem energies, as this is a more complicated analysis than the range finder above. If any is identified, run the drawBraggPeakGraphFit at that specific degrader thickness to see where the problems are.
Displaying the results
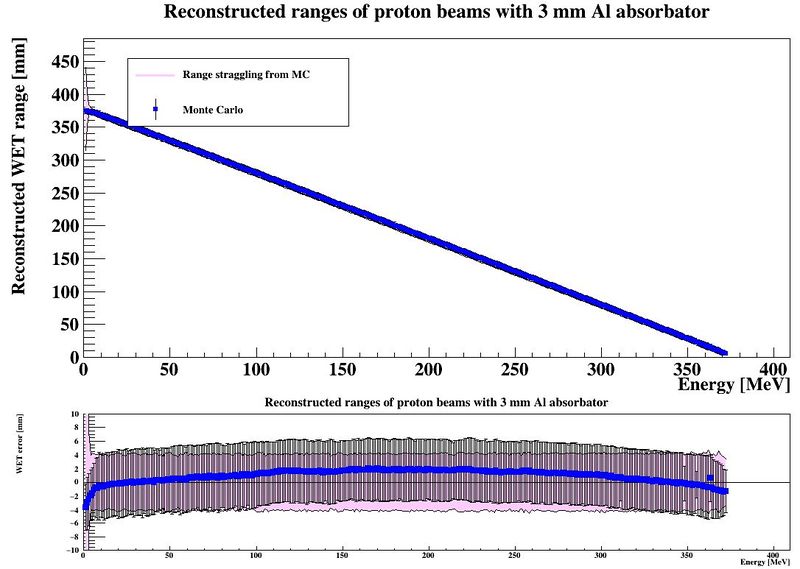
If there are no problems, use the script DTCToolkit/Scripts/makePlots.C to plot the contents of the file DTCToolkit/OutputFiles/results_makebraggpeakfit.csv:
[DTCToolkit] $ root Scripts/makePlots.C
The output is a map of the accuracy of the range determination, and a comparison between the range resolution (#sigma of the range determination) and its lower limit, the range straggling.
